합성곱 신경망 ( CNN, Convolutional Neural Network )

CNN, Convolutional Neural Network

CNN은 합성곱(Convolution) 연산을 사용하는 ANN의 한 종류다.

Convolution을 사용하면 3차원 데이터의 공간적 정보를 유지한 채 다음 레이어로 보낼 수 있다.

대표적인 CNN으로는 LeNet(1998)과 AlexNet(2012)이 있다.

VGG, GoogLeNet, ResNet 등은 층을 더 깊게 쌓은 CNN기반의 심층 신경망(DNN)이다.

CNN의 네트워크 구조

지금까지 다룬 신경망은 이전 계층의 모든 뉴런과 결합되어 있었고, 이를 Affine layer라고 불렀다.

이런 식으로 이전 계층의 모든 뉴런과 결합된 형태의 layer를 fully-connected layer(FC layer, 전결합 레이어) 또는 Dense layer라고 한다. 

CNN에서는 FC 대신 다음 두 레이어를 활성화 함수 앞 뒤에 배치한다.

• Convolutional layer
• Pooling layer

그러나 모두 이렇게 바뀌는 것은 아니고 출력에 가까운 층에서는 FC layer를 사용할 수 있다.

또한 마지막 출력 계층에서는 FC - Softmax 그대로 간다.

결과적으로 다음과 같은 형태가 된다.

... Conv - ReLU [- Pooling] ... 반복 ... FC - ReLU ... FC - Softmax

* Pooling layer는 생략하기도 한다.

FC layer의 문제점

전결합 레이어는 1차원 데이터만 입력 받을 수 있기 때문에, 3차원 데이터를 평탄화 해서 입력해야 한다.

여기서 3차원 데이터의 공간적 정보가 소실된다는 문제가 발생한다.

예를 들어 MNIST 이미지는 형상이 (1채널, 가로 28픽셀, 세로 28픽셀)인 3차원 데이터였다. 

이 3차원 데이터에는 공간적으로 가까운 픽셀은 값이 비슷하다거나, RGB의 각 채널은 서로 밀접하게 관련되어 있다든가 하는 공간적 정보가 들어있다.

이를 Affine layer에 입력할 때, (1, 784)의 1차원 데이터로 평탄화 해서 넘기기 때문에 이런 공간적 정보가 소실된다.

* (1, 784)는 2차원 배열이지만, 1은 이미지 1개를 의미하고, 이미지 1개의 데이터는 784에 들어있는 것이므로 이미지 자체는 1차원 데이터 784에 들어있다.

반면 CONV layer는 형상을 유지한다. 입/출력 모두 3차원(배치처리 시 4차원) 데이터로 처리하기 때문에 공간적 정보를 유지할 수 있다.

왼쪽은 일반적인 3-layer Neural Network(전결합), 오른쪽은 CNN을 3차원으로 표현한 그림이다.

 

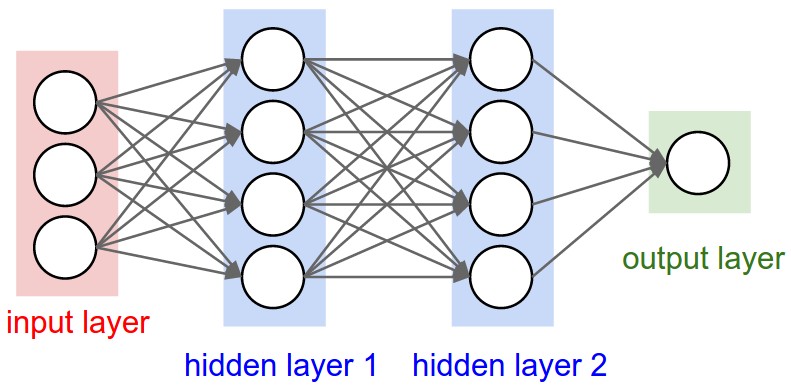
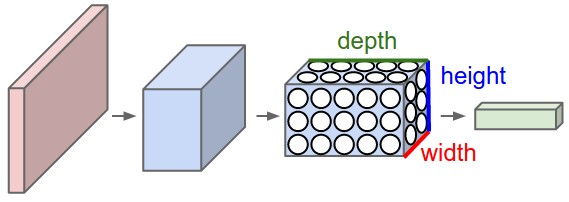
Convolutional layer

Convolution은 합성곱이라는 뜻이다.

합성곱은 "두 함수 중 하나를 반전(reverse)하고 이동(shift)시켜가며 다른 하나의 함수와 곱한 결과를 적분해나간다." 는 뜻이기는 한데 잘 와닿지 않으므로 다음 그림을 보자.

2차원 데이터의 합성곱 연산:

<출처 : http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution>

* 출력이 Convolved Feature. CNN에서는 합성곱 계층의 입출력 데이터를 특징 맵(feature map)이라고 부른다. 

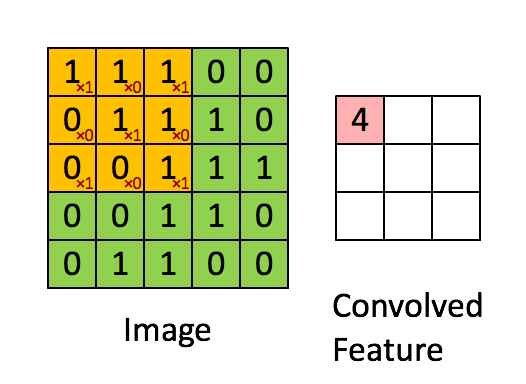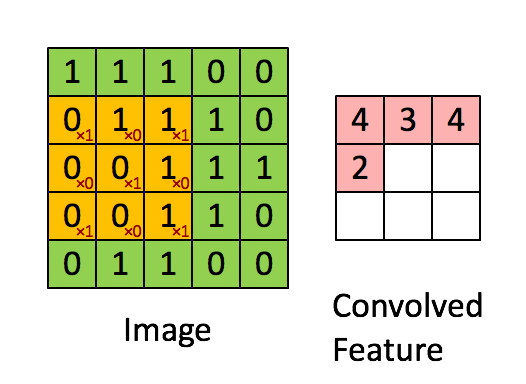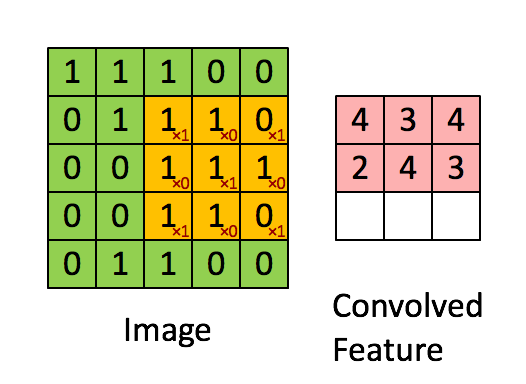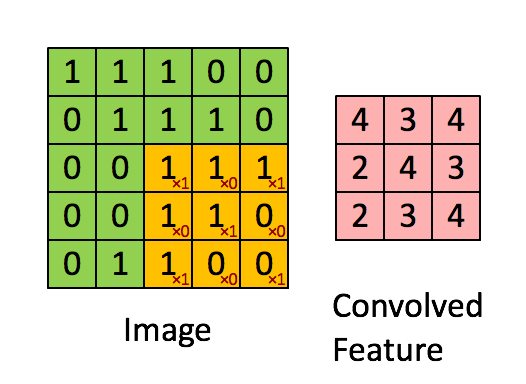
위 합성곱의 정의에서 두 함수를 이미지, 필터라고 생각하면, 필터를 이동시켜가며 이미지와 곱한 결과를 적분(덧셈)해 나간다는 뜻이 된다.

* 여기서 수행하는 적분(덧셈)은 단일 곱셈-누산(fused multiply-add, FMA)이라 한다.

* 행렬에서 반전(reverse)에 대응하는 것은 플리핑(flipping)인 듯. 사실 flipping하면 합성곱 연산이고 안하면 교차상관 연산인데 딥러닝에서는 잘 구분하지 않는다. 안해도 합성곱으로 본다. flipping 여부를 인수로 받기도 함.

* 필터를 커널이라고 하기도 한다.

* 편향은 필터를 적용한 결과 데이터에 더해진다. 편향은 항상 (1x1)이며 이 값을 모든 원소에 더한다.

Padding

1만큼 패딩했다고 하면, 입력 데이터 사방 1픽셀을 특정 값으로 채워 늘리는 것을 의미한다.

주로 출력 크기를 조정할 목적으로 사용한다.

예를 들어 위 그림에서 (5, 5) 데이터에 (3, 3) 필터를 적용했더니 출력이 (3, 3)이 되었다.

이처럼 합성곱 연산을 거칠 때 마다 크기가 작아지게 되는데 출력 크기가 너무 줄어드는 것을 막기 위해 패딩을 사용한다.

패딩을 사용하면 그만큼 입력 데이터를 크게 만들어 출력 데이터를 입력 데이터와 동일한 형상으로 조정할 수 있으므로

입력 데이터의 공간적 크기를 고정한 채로 다음 계층에 전달할 수 있다.

Stride

필터를 적용하는 간격을 스트라이드(stride)라고 한다.

stride=2이면 두 칸씩 건너 뛰면서 필터를 적용한다.

출력 크기 계산

입력 크기를 (H, W), 필터 크기를 (FH, FW), 출력 크기를 (OH, OW), 패딩을 P, 스트라이드를 S라 하면

출력 크기는 다음과 같다.

           

이 때 OH, OW는 정수로 나누어 떨어지는 값이어야 하지만,

딥러닝 라이브러리에서는 가까운 정수로 반올림 하는 등 에러내지 않고 진행하는 경우도 있다.

수식이 직관적으로 이해가 안되면, (8x4)행렬에 (2x2)필터를 적용시켜본다. 

이리저리 하다보면 필터가 몇 번 적용되느냐는 필터의 크기보다는 stride가 얼마이냐가 결정한다는 것을 알 수 있다. 

필터를 위에서부터 적용했을 때 필터의 크기는 맨 마지막에 필터가 들어갈 수 있느냐에만 관여하게 된다.

만약 필터를 모든 입력데이터의 원소에 한 번씩만 적용해야 한다면 stride=필터의 크기가 된다. 

그래서 결국, 필터가 몇 번 들어가느냐는 stride가 크게 좌우한다.

3차원 데이터의 합성곱 연산

위쪽에 첨부한 그림은 2차원 데이터의 합성곱 연산이다. 

이미지는 3차원 데이터이기 때문에, 3차원 합성곱 연산을 수행해야 한다.

다음 이미지는 3차원 배열을 (Height, Width, Channel) 순서로 나타냈다.

<출처 : CS231n>

*하나의 Channel은 하나의 2차원 배열(행렬)이라고 생각하면 편하다.

Input은 3개의 Channel을 가지고 있는데, 각각의 Channel 당 하나의 필터 Channel이 적용되었다.

즉, 하나의 입력 채널에는 하나의 필터 채널이 필요하다.

이는 입력 데이터의 채널 수와 필터의 채널 수가 일치해야 한다는 것을 의미한다.

Output Volumn은 (3, 3, 2)로, 첫번째 output 채널은 필터 W0을 적용한 결과이고 두번째 output 채널은 필터 W1을 적용한 결과이다. 

각각의 필터 채널에서 연산한 값을 모두 더한 값이 output 채널이 된다. 필터 채널이 얼마가 있든, 결국 다 더해져 하나의 output 채널을 구성한다.

따라서 output 채널의 수는 필터 채널의 수와는 관련 없고, 필터가 몇 개 있느냐가 결정한다.

또한 각 필터 채널에서 연산한 값을 모두 더해야 하므로 모든 채널의 필터는 같은 크기여야 한다.

예를 들어, 필터가 하나만 있으면 output은 채널의 수가 1개다. 2차원 배열(행렬) 하나가 output이다.

여기서는 W0, W1 두 개 있으니 output 채널이 2다.

이를 수식으로 나타내면 다음과 같다. 

여기서는 위 이미지와 달리 (Number(개수), Channel, Height, Width) 순서로 나타냈다.

이런식으로 왼쪽을 고차원, 오른쪽을 저차원으로 나타내야 생각하기 편하다.

(C, H, W)  *  (FN, C, FH, FW)  →  (FN, OH, OW)

편향을 추가한 수식은 다음과 같다.

편향은 각각의 output 필터에 적용되는거니까, output 채널만큼 있어야 한다. 

하나의 편향 채널은 단일 값이며 이 값이 하나의 output 채널의 모든 원소에 더해진다.

(FN, OH, OW) + (FN, 1, 1) → (FN, OH, OW)

배치처리를 추가한 수식은 다음과 같다.

N개의 배치를 받게 되어도 가중치는 각각에 적용되는 거니까 필터와 편향은 변함없고, output 개수만 N개로 늘어난다.

(N, C, H, W)  *  (FN, C, FH, FW) → (N, FN, OH, OW) + (FN, 1, 1) → (N, FN, OH, OW)

* TensorFlow에서 사용하는 경우 순서를 조금 다르게 나타낸다.

(N, H, W, C)  *  (FH, FW, C, FN) → (N, OH, OW, FN) + (1, 1, FN) → (N, OH, OW, FN)

결국 CNN에서 각 계층을 타고 흐르는 데이터는 4차원 형상이다.

Pooling layer

풀링은 가로/세로 방향의 공간을 줄이는 연산이다.

max pooling(최대 풀링)과 average pooling(평균 풀링)이 있는데, 이미지 인식 분야에서 주로 사용하는 것은 max pooling이라 그냥 풀링이라고 하면 보통 최대 풀링을 의미한다.

2x2 max pooling을 적용한 이미지.

<출처 : wiki>

보통 풀링의 window size와 stride는 같은 값으로 설정해서 모든 원소가 한 번씩만 연산에 참여하도록 한다.

여기서는 window size가 2x2, stride는 2다.

Pooling layer는 다음과 같은 특징을 지닌다.

• 학습해야 할 매개변수가 없다.
• 채널 수가 변하지 않는다.
  Conv layer에서는 각 필터 채널을 적용한 결과 채널들을 다 더해야 하나의 output 채널이 되지만, Pooling layer에서는 결과를 더하지 않는다. 결과 채널이 그대로 output 채널이 되기 때문에 채널 수가 그대로다.
• 입력 데이터의 변화에 민감하게 반응하지 않는다.(Robustness)
  pooling layer를 적용하는 목적이 여기에 있는데 내가 찾아내고자 하는 특징의 위치를 중요하게 여기기 보다는, input이 그 특징을 포함하고 있느냐 없느냐를 판단하도록 하기 위해서 주변에 있는 값들을 뭉뚱그려서 보겠다는거다.

CNN 구현

CNN에서 계층 사이에 전달되는 데이터는 4차원이라는 점에 유의한다. (N, C, H, W)

im2col (image to column)

im2col을 사용하면 반복문을 여러개 사용하지 않아도 4차원 데이터의 합성곱 연산을 수행할 수 있다.

im2col은 caffe, tensorflow 등의 프레임워크에서 지원하는 함수로 입력 데이터를 필터를 적용하기 좋은 형태(행렬)로 전개하는 함수다.

numpy에 반복문을 사용하면 성능이 떨어지게 되는데, im2col을 사용해 행렬로 전개하게 되면 행렬 계산을 처리하게 되므로 성능에 이점이 있고 편리하기도 하다.

Conv layer 구현

3차원(배치처리 시 4차원) 입력 데이터에 im2col을 사용하면, 3차원 필터 1개를 1회 적용하는 영역(입력 데이터의 일부인 3차원 영역)을 한 row로 하는 행렬로 변환한다.

```python

col_x = im2col(x, FH, FW, self.stride, self.pad)

```

변환된 행렬의

row 개수(Height)는 필터 적용 횟수 = 출력 맵의 2차원 크기 = OH * OW

column 개수(Width)는 C * FH * FW

같은 방식으로 필터도 행렬로 전개하는데, 이 때 im2col을 사용할 필요는 없고, 그냥 reshape 사용하면 된다.

입력 데이터와는 조금 다른게, 배치처리를 하지 않은 단일 3차원 입력 데이터에 대해서 필터 FN개를 적용하게 되므로 3차원 필터 1개를 row로 하는 행렬로 변환한다. 그래야 Transpose한 다음 입력 데이터를 변환한 행렬과 곱했을 때, 필터 적용 영역과 곱하게 된다. 그래서 reshape(FN, -1).T 형태로 전개한다.

변환된 행렬의

row 개수(Height)는 FN

column 개수(Width)는 C * FH * FW

연산을 위해서 필터를 변환한 행렬을 Transpose한 다음 둘을 곱하면 

(OH * OW , C * FH * FW) * (C * FH * FW , FN) = (OH * OW , FN)

이고, 각각의 필터 적용 영역에 해당 필터를 곱하게 되어 합성곱 연산과 동일한 결과가 나온다.

여기에 편향을 더해준다. (OH * OW , FN) + (FN, )

편향은 데이터를 전개한 행렬에 더하게 되므로 (FN, 1, 1)이 아니라 1차원 배열이어야 브로드캐스트가 제대로 동작한다.

(FN, 1, 1)을 더하고 싶다면 4차원으로 reshape한 다음 더해야한다.

또한 grads['b']가 역전파로부터 구한 .db 값이므로 1차원 배열이라서, 이도 3차원으로 reshape해줘야 기울기 갱신 시 에러가 발생하지 않는다.

마지막으로 이를 reshape한다. (OH * OW , FN) → (FN, OH, OW)

배치처리했을 경우 앞에 N만 붙여주고 마지막에 4차원으로 reshape하면 된다.

(N * OH * OW , C * FH * FW) * (C * FH * FW , FN) = (N * OH * OW , FN)

(N * OH * OW , FN) + (FN, )

(N * OH * OW , FN) → (N , OH, OW, FN) → (N , FN, OH, OW)

reshape할 때 주의할 점은 바로 (N * OH * OW , FN) → (N , FN, OH, OW)하면 안되고

(N , OH, OW, FN)으로 reshape한 다음 차원의 순서를 변경해야 한다.

```python

result_2d.reshape(N, OH, OW, FN).transpose(3, 0, 1, 2)

```

사실 이런거 잘 몰라도, 그냥 im2col 호출하면 알아서 해주니까 입력 데이터에 im2col 사용하고, 

필터에 reshape(FN, -1).T 사용한 다음 둘을 곱한 결과를 4차원으로 reshape().transpose()하면 끝이다.

역전파

역전파는 순전파에서 행렬곱을 사용했기 때문에 Affine layer의 역전파와 동일하게 처리하면 된다.

마지막에 col2im으로 행렬을 다시 4차원 데이터로 만들어 리턴한다.

Pooling layer 구현

Conv layer처럼 im2col을 사용해서 전개한다.

그러나 Pooling은 각 채널마다 output 행렬이 나오기 때문에, Conv layer 처럼 각 채널의 연산 결과를 합산하지 않아야 한다.

그래서 2차원 풀링 연산 1개(행렬)를 1회 적용하는 영역(입력 데이터의 1개 채널의 일부인 2차원 영역)을 한 row로 하는 행렬로 reshape한다.

```python

col = col.reshape(-1, self.pool_h*self.pool_w)

```

이렇게 하면 전개한 행렬에서 ``python np.max(col, axis=1)``를 사용하면 각 row별 최댓값을 반환받을 수 있다.

그리고 나서 reshape한 후 transpose해야한다.

```python

out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

```

im2col을 사용하면 여러 채널의 데이터가 한 row에 들어오게 되는데,

그렇기 때문에 이를 reshape 했을 때 데이터가 채널 별로 모여있는게 아니라 채널 각각에 적용한 순서대로 모여있다.

그래서 일단 max를 각 row에 대해 구한 후 reshape하고, transpose로 채널 별로 정렬한다.

역전파

ReLU처럼 값을 통과시키느냐(최댓값), 안시키느냐(나머지)의 문제이기 때문에 ReLU layer의 역전파와 동일하게 처리하면 된다.

CNN 시각화

<AlexNet의 첫번째 필터를 이미지로 나타낸 사진, cs231n>

각각의 필터는 같은 입력을 받아 같은 연산을 거쳐 갱신되지만, 초깃값을 모두 다르게 설정해놓았기 때문에 갱신된 후 필터가 가지는 값은 서로 다르다.

만약 필터의 초깃값을 모두 동일하게 설정해놓았다면, 가중치가 똑같이 갱신되어 같은 모양이 나오게 된다.

이것이 필터의 초깃값을 무작위로, 서로 다르게 설정해야 하는 이유다.

첫번째 필터는 edge(색상이 바뀌는 경계)와 blob(국소적으로 덩어리진 영역)을 학습하여, 입력 데이터로부터 이를 잡아낸다.

무작위로 초기화 된 필터가, 학습했더니 이런 모양이 되는 것이다.

AlexNet의

1번째 Conv layer에서는 Edge와 Blob을 잡아내고,

3번째 Conv layer에서는 texture를,

5번째 Conv layer에서는 Object Parts를, 

8번째 FC layer에서는 Object Classes를 잡아낸다.

이렇게 layer를 거듭할 수록 더 추상적인 정보를 잡아내게 된다. 

즉, 뉴런이 반응하는 대상이 단순한 패턴에서 사물의 의미를 나타내는 고급정보로 변화한다.

층을 깊게 쌓을 수록 더 추상적인 정보를 추출할 수 있고, 이런 장점을 극대화하기 위해 층을 deep하게 쌓은게 딥러닝이다.

위 사진의 필터들은 color인 것도 있고 grayscale인 것도 있는데, 이는 AlexNet에서 입력 데이터를 두 개의 프로세싱 스트림으로 나눠 처리하기 때문이다. 하나는 high-frequency, 이게 grayscale이고 다른 하나가 low-frequency, 이게 color features.

이미지에서 말하는 frequency는 pixel 값의 변화량을 의미한다. 변화량은 색상이 주변에 비해서 얼마나 변했느냐라고 생각하면 된다. high-frequency filter는 pixel의 변화량이 큰 지점을 잡아내기 때문에 그림의 경계를 잡아내고, low-frequency filter는 변화량이 작은 지점을 잡아내는 거니까 그림에서 국소적으로 덩어리진 영역을 잡아낸다.

참고

• 밑바닥부터 시작하는 딥러닝
• http://cs231n.github.io/convolutional-networks/