선형 시간 안에 중앙값 선택하기

 

최악의 경우에도 선형 시간에 중간값을 선택할 수 있는 알고리즘은 다음과 같다.

 

* 아래는 median을 찾는 예이지만, k번째 작은 값 찾는 문제에 적용 가능하다.

``c Element select(SetOfElements S, int k)``

• 중앙값만 찾는 거라면 k 파라미터가 필요 없지만, 일반적인 선택 문제로 확장하면 k 파라미터가 필요함.
• k는 몇번째로 큰 값을 찾을건지. k번째로 작은 값을 찾는다. `` k=n/2`` 를 넘기면 중간값을 찾겠다는 것.

 

알고리즘 (k번째 작은 값 찾기를 이용해 median 찾는 예제)

1. 입력 배열이 n개라면 원소 5개짜리 \\(\lceil n/5 \rceil\\) 그룹으로 나눈다.

• 마지막 집합은 \\(n \mod 5\\)개 원소를 가질 수 있다.

 

2. 각 그룹에서 중앙값(`` _m``)을 찾는다. 중앙값을 찾는 데는 다음 방법을 사용한다.

• 2018/05/03 - [Algorithm/Theory] - 5개의 원소를 7번 비교로 정렬하기 / 6번 비교로 중간값 찾기

 

3. 이제 중앙값들의 중앙값(median of median, `` m``)을 찾아야 하는데, 어차피 이도 중앙값을 찾는 문제이므로 ``c select()``를 한 번 재귀호출한다. ``c m = select(M, M/2);`` 

• `` M``은 `` _m``들로 이루어진 집합(배열)을 의미한다.
• `` M/2``를 넘기므로 개수가 짝수일 경우 내림 되어 `` m``은 더 앞에 있는 중앙값이 된다.

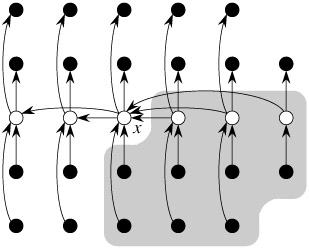
4. (`` x=m``) x를 기준으로 x보다 큰 원소는 `` S1`` 그룹, x보다 작은 원소는 `` S2`` 그룹으로 분할한다.

• x를 기준으로 [우측 & 하단](회색영역)에 있는 모든 원소는 x보다 크다. -> `` S2``
• x를 기준으로 [좌측 & 상단]에 있는 모든 원소는 x보다 작다. -> `` S1``
• 나머지 영역[우상단&좌하단]에 대해서는 대소를 알 수 없으므로 x와 직접 비교해 알맞은 그룹으로 넣는다.

 

5. 분할 정복으로 해결한다.

* 중간값 찾는 경우 `` k = n/2`` 가 된다.

```c

if (k == sizeof(S1) + 1)

    return m;

else if (k <= sizeof(S1))  // k번째 작은 값을 찾을건데 S1에 원소 개수가 k보다 크다면? k번째 작은 값은 S1에 있다.

    return select(S1, k);

else

    return select(S2, k - (sizeof(S1) + 1));

```

 

수행 시간 분석

계산이 간단하도록 n이 5의 홀수 배라고 가정한다.

 

1-2. 5개의 키 집합들에 대한 중앙값을 구하는 데는 5개의 원소의 중앙값을 찾는데 6번 비교하는 알고리즘을 사용했다고 가정하면 \\(6*(n/5)\\)번 비교.

 

3. 중앙값들의 중앙값을 찾는데 재귀를 사용하기 때문에 \\(W(n/5)\\)번 비교.

 

4. x를 기준으로 확실히 x보다 작은 원소의 개수는

\\[(\frac{n}{5} - 1) \frac{1}{2} 3 + 2 = \frac{3n}{10} + \frac{1}{2} \\]

x보다 확실히 큰 원소의 개수도 n이 5의 홀수배이면 위와 같다.

따라서 대소를 알 수 없는 영역에 속하는 원소의 개수는 \\( \approx 4n/10 \\) 이므로, 이 만큼 비교.

 

5. 분할 정복법으로 ``c select()``를 재귀 호출 하는데, 최악의 경우는 예를들면 찾으려는 k가 `` S1``에 속해있는데 대소를 알 수 없는 영역을 비교해보았더니 모든 원소가 x 보다 작아 `` S1``에 들어가는 경우이다.

\\( S1.size = 3n/10 + 4n/10 \\) 이 되므로 \\(W(7n/10)\\) 만큼 비교.

 

\\[W(n) \le \frac{6n}{5} + W(\frac{n}{5}) + \frac{4n}{10} + W(\frac{7n}{10})\\]

점화식을 푸는데 재귀 트리를 이용해도 좋고(Computer Algorithms, Sara Baase)

수학적 귀납법을 이용해도 된다.(Introduction to algorithms)

재귀트리를 이용해 구해보면 \\(16n\\)이 나오는데, 최악의 경우 \\(2.95n\\)번 비교하는 알고리즘도 존재하기는 하나 꽤 복잡하다.

in-place는 아니지만 재귀의 깊이가 \\(O(\lg{n})\\)이므로 공간적인 부분이 많이 필요하지는 않다.

 

하한선

현재 최선의 하한선은 \\(2n\\) 정도로 알려져 있다.