피어슨 상관 계수 (Pearson Correlation Coefficient)
상관계수(correlation coefficient)란 두 변수가 어떤 상관 관계를 가지는가?를 의미하는 수치다.
+1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다.

X와 Y 사이의 피어슨 상관 계수를 구하는 식은 다음과 같다
\\[r_{XY} = \frac{ \sum^n_i (X_i - \bar{X})(Y_i - \bar{Y}) }{ \sqrt{\sum^n_i (X_i - \bar{X})^2} \sqrt{\sum^n_i (Y_i - \bar{Y})^2} } \\]
여기서 X, Y는 vector인데
식을 조금 들여다보면 결국 다음과 같은 과정이다.
1. 각 vector의 표본평균\\(\bar{A}\\)를 구해서 A의 0이 아닌 각 원소에 빼주어 normalization하고,
2. normalized 된 vector들 사이의 cosine similarity를 계산한다.
피어슨 상관 계수는 다양한 상황에서 쓰이지만,
normalized된 cosine similarity를 계산하는 것이기 때문에 피어슨 상관 계수를 similarity로도 해석할 수 있다.
피어슨 상관 계수가 similarity로 쓰이는 예로는 추천 시스템이 있다.
추천 시스템에서 collaborative filtering 방식을 사용할 때는 User-user 간, 또는 Item-item 간 similarity를 계산해야 한다.
이 때 피어슨 상관 계수를 similarity로 사용하게 된다.
유저 A와 비슷하게 영화를 평가한 유저를 찾기 위해서 user A와 나머지 유저들의 similarity를 계산하려고 한다.
| movie 1 | m2 | m3 | m4 | m5 | m6 | m7 | |
| user A | 4 | 5 | 1 | ||||
| user B | 5 | 5 | 4 | ||||
| ... |
(평가하지 않은 항목은 0으로 집계되기 때문에 cosine similarity를 사용하게 되면 미평가 항목이 곧 안좋게 평가한 항목과 동일하게 간주된다는 문제가 있어 피어슨 상관 계수를 사용한다.)
피어슨 상관 계수를 계산해보면
\\(\bar{A} = \frac{4+5+1}{3} = \frac{10}{3} \\) \\(\bar{B} = \frac{14}{3} \\)
\\(A - \bar{A} = [\frac{2}{3}, 0, 0, \frac{5}{3}, -\frac{7}{3}, 0, 0]\\)
\\(B - \bar{B} = [\frac{1}{3}, \frac{1}{3}, -\frac{2}{3}, 0, 0, 0, 0]\\)
이제 이 둘의 cosine similarity를 계산하면 피어슨 상관 계수가 되고, 이는 곧 sim(A, B)가 된다.
\\(sim(A, B) = 0.092\\)
상관계수를 해석할 때 주의할 점
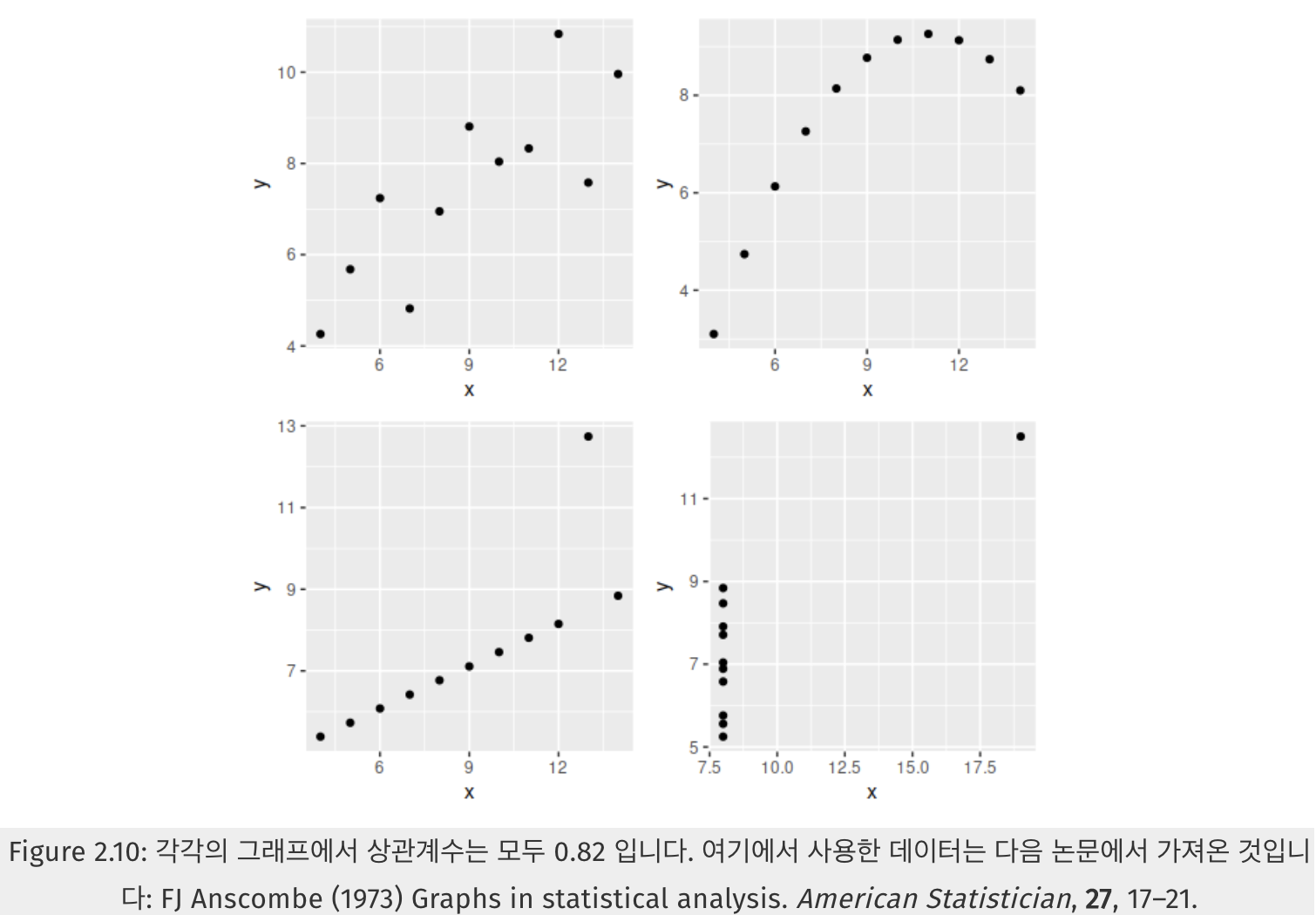
상관계수(correlation coefficient)는 선형관계의 강도만 측정하기에, 종종 오해로 이어질 수 있습니다.
아래 그래프는 모두 0.82의 상관계수를 갖습니다만, 나타나는 관계는 아주 다릅니다. 이를 통해 상관계수값에만 의존하지 말고 데이터를 그려서 살펴보는 것이 얼마나 중요한지 알 수 있습니다.
'Machine Learning > Theory' 카테고리의 다른 글
| Website for public datasets (0) | 2019.09.10 |
|---|---|
| 민감도와 특이도 (sensitivity, specificity) (0) | 2019.05.24 |
| 재표본추출 방법, Resampling Methods (0) | 2019.05.20 |
| 분류, Classification (0) | 2019.05.07 |
| 선형 회귀, Linear Regression (0) | 2019.05.07 |